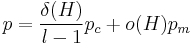Holland's schema theorem

Holland's schema theorem is widely taken to be the foundation for explanations of the power of genetic algorithms. It was proposed by John Holland in the 1970s.

A schema is a template that identifies a subset of strings with similarities at certain string positions. Schemata are a special case of cylinder sets; and so form a topological space.

Description

For example, consider binary strings of length 6. The schema 1*10*1 describes the set of all strings of length 6 with 1's at positions 1, 3 and 6 and a 0 at position 4. The * is a wildcard symbol, which means that positions 2 and 5 can have a value of either 1 or 0. The order of a schema is defined as the number of fixed positions in the template, while the defining length 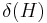$\delta(H)$ is the distance between the first and last specific positions. The order of 1*10*1 is 4 and its defining length is 5. The fitness of a schema is the average fitness of all strings matching the schema. The fitness of a string is a measure of the value of the encoded problem solution, as computed by a problem-specific evaluation function. Using the established methods and genetic operators of genetic algorithms, the schema theorem states that short, low-order schemata with above-average fitness increase exponentially in successive generations. Expressed as an equation:

$\operatorname{E}(m(H,t%2B1)) \geq {m(H,t) f(H) \over a_t}[1-p].$

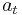Here $m(H,t)$ is the number of strings belonging to schema $H$ at generation $t$ , $f(H)$ is the observed fitness of schema $H$ and $a_t$ is the observed average fitness at generation $t$ . The probability of disruption $p$ is the probability that crossover or mutation will destroy the schema $H$ . It can be expressed as:

$p = {\delta(H) \over l-1}p_c %2B o(H) p_m$

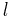where $o(H)$ is the number of fixed positions, $l$ is the length of the code, 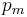$p_m$ is the probability of mutation and 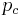$p_c$ is the probability of crossover. So a schema with a shorter defining length 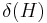$\delta(H)$ is less likely to be disrupted.
An often misunderstood point is why the Schema Theorem is an inequality rather than an equality. The answer is in fact simple: the Theorem neglects the small, yet non-zero, probability that a string belonging to the schema $H$ will be created "from scratch" by mutation of a single string (or recombination of two strings) that did not belong to $H$ in the previous generation.

References

J. Holland, Adaptation in Natural and Artificial Systems, The MIT Press; Reprint edition 1992 (originally published in 1975).
J. Holland, Hidden Order: How Adaptation Builds Complexity, Helix Books; 1996.